edit Answer person Parthasaradhi M Member since Recommend (0) Comment (0) person Kishore Kumar Hence x 3 y 3 z 3 3xyz = ½ (x y z) (xy) 2 (yz) 2 (zx) 2 Recommend (0) Comment (0)Zeroes of a polynomial Motivate and State the Remainder Theorem with examples Statement and proof of the Factor Theorem Factorization of ax2 bx c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem x 3 y 3 z 3 3xyz = (x y z) (x 2 y 2 z 2 xy yz zx) and their use in ⇒ x 3 y 3 z 3 = 3xyz That is (a – b) 3 (b – c) If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____ formula of polynomials Questions;

Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In
X^3+y^3+z^3-3xyz formula proof
X^3+y^3+z^3-3xyz formula proof-Click here👆to get an answer to your question ️ Factorize x^3 y^3 z^3 = 3xyzFactoring by pulling out fails The groups have no common factor and can not be added up to form a multiplication Final result x 3 y x 3 z xy 3 xz 3 y 3 z yz 3




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top
대수 인수분해하기 x^3y^3z^3 x3y3 z3 x 3 y 3 z 3 x3y3 x 3 y 3 을 (xy)3 ( x y) 3 로 바꿔 씁니다 (xy)3 z3 ( x y) 3 z 3 두 항 모두 완전세제곱식이므로 세제곱의 합 공식 a3 b3 = (ab)(a2 −abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) 을 이용하여 인수분해합니다 이 때 a = xy a = x y #x^3y^3z^33xyz=x^3y^33x^2y3xy^2z^33xyz3x^2y3xy^2=(xy)^3z^33xy(xyz)=(xyz)((xy)^2z^2(xy)z)3xy(xyz)=(xyz)(x^22xyy^2z^2xyxz3xy)=(xyz)(x^2y^2z^2xyyzzx)# Answer link Related questions Revision of algebraic expressions Formula Statement and proof of the Factor Theorem x̣ 3 y 3 z 33xyz (x̣yz) 2 = x 2 y 2 z 2 2x̣y 2yz 2zx̣ (x̣y) 3 = x 3 y 3 3x̣y (xy) x̣ 3 y 3 z 3 – 3xyz = (xyz) (x 2 y 2 z 2xyyzzx) x̣ 3 y 3 = x 3 y 3 = (xy)(x 2 xyy 2) LINEAR EQUATIONS IN TWO VARIABLES
All positive integers N other than those div by 3 but not by 9 are representable as N = x 3 y 3 z 33xyz with integral x,y,z => 0 The primes (other than 3) are representable in this manner in one and only one way (Carmichael)15 Show that the curves x 3 − 3xy 2 = c, where c Φ 0, and 3x 2 y − y 3 = d, d Φ 0, intersect at right angles 16 Show that the two families of curves and are orthogonal families; If xy z=0 then prove that x 3 y 3 z 3 =3xyz Get the answers you need, now!
CBSE NCERT Notes Class 9 Maths Polynomials Show Topics Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x 3 y 3 z 3 = 3xyz Hence, xyz= 0 x 3 y 3 z 3 = 3xyz Answered by 4th Jun, 14, 0323 PM Concept Videos Listing of algebraic identities for cubic Polynomials and simplify the comp Listing of algebraic identities for cubic Polynomials and simplify the comp Statement and proof of the Factor Theorem x 3 y 3 z 33xyz CHAPTER NAME – LINEAR EQUATIONS IN TWO VARIABLES TOPICS REMOVED – Examples, problems on Ratio and Proportion UNIT IIICOORDINATE GEOMETRY CHAPTER NAME – COORDINATE GEOMETRY TOPICS REMOVED – No deletion UNIT IVGEOMETRY CHAPTER NAME – INTRODUCTION TO




Integrated Inequalities Abstract Algebra Teaching Mathematics




Let X Be The Am And Y Z Be Two Gms Between Two Positive Numbers Then Y3 Z3 Xyz Is Equal To A 1 B 2 C 1 2 D None Of
Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z =In this video I am going to show you how to prove x3y3z3= 3xyzThis is special identities of class 9This identities can also prove in other way Link of thi




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top




Prove That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In
Motivate and State the Remainder Theorem with examples Statement and proof of the Factor Theorem x 3 y 3 z 33xyz LINEAR EQUATIONS IN TWO VARIABLES Examples, problems on Ratio and Proportion UNIT IIICOORDINATE GEOMETRY Chapter Topics COORDINATE GEOMETRY No deletion UNIT IVGEOMETRY Chapter Topics INTRODUCTION(x1) (x2) = x 2 3x 2Related Wiki Ask Scroll Like NextGurukul




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



If X 3 Y 3 3axy 0 Then Prove That D 2y Dx 2 2a 2xy Ax Y 2 3 Sarthaks Econnect Largest Online Education Community
The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example; Statement and proof of the Factor Theorem x 3 y 3 z 33xyz CHAPTER NAME – LINEAR EQUATIONS IN TWO VARIABLES TOPICS REMOVED – Examples, problems on Ratio and Proportion UNIT IIICOORDINATE GEOMETRY CHAPTER NAME – COORDINATE GEOMETRY TOPICS REMOVED – No deletion UNIT IVGEOMETRY CHAPTER NAME – INTRODUCTION TO// dansmath is on your side!




Polynomials Ppt Video Online Download



1
If xyz=0 then prove that x^3y^3z^3 = 3xyz Ask questions, doubts, problems and we will help youVerify that `x^3y^3z^33x y z=1/2 (xyz) (xy)^2 (yz)^2 (zx)^2` Verify that `x^3y^3z^33x y z=1/2 (xyz) (xy)^2 (yz)^2 (zx)^2` Watch later Share Copy linkX∂u ∂x y∂u ∂y z∂u ∂z where u = x3y3z3 x3 y3 z3 euler theorem ADD COMMENT 1 Answer 1 94 views written 50 years ago by shailymishra30 ♦ 330 Statement If u=f (x, y, z)is a homogeneous function of degree n, then x∂u ∂x y∂u ∂y z∂u ∂z = n ⋅ u




If X Y Z 0 Then X 2 Yz Y 2 Zx Z 2 Xy Equals A 1 B 2 C 3 Brainly In




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer
to prove x 3 y 3 z 3 =3xyz x 3 y 3 z 3 3xyz= (xyz) (x 2 y 2 z 2 xyyzzx)Click here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx) Algebraic Identities Of Polynomials Example Problems With Solutions Example 1 Expand each of the following Solution (i) We have, Example 2 Find the products (i) (2x 3y) (2x – 3y) Solution (i) We have, Example 3 Evaluate each of



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora



Cbse 9 Math Cbse Polynomials Ncert Solutions
Describe the curves of each family and sketch several of them (Hint consider the It is usually best to see how we use these two facts to find a potential function in an example or two Example 2 Determine if the following vector fields are conservative and find a potential function for the vector field if it is conservative →F = (2x3y4 x)→i (2x4y3 y)→j F → = ( 2 x 3 y 4 x) i → ( 2 x 4 y 3 y) j → =x 3 xy 2 xz 2x 2 yxyzzx 2 x 2 yy 3 yz 2xy 2y 2 zxyz x 2 zy 2 zz 3xyzyz 2xz 2 =x 3 y 3 z 3xyzxyzxyz = x 3 y 3 z 3 3xyz LHS=x 3 y 3 z 3 3xyz LHS=RHS So it is proved I am sure thats the wayI studied soI'm in 9th




Verify That X Cube Y Cube Z Cube 3xyz 1 2 X Y Z X Y Square Y Z Square Z X Square Brainly In



Http Www Cis Umac Mo Fstitl Calculus12 13 Example 04 Pdf
Assume instead that x, y, z ∈ Z ∖ {0} satisfy the equation (replacing z by − z ) x3 y3 z3 = 0, with x, y and z pairwise coprime (Clearly at least one is negative) One of them should be even, whereas the other two are odd Assume z to be even Then x and y are oddOne proof of the AMGM inequality uses the fact that f (x) = log(x) is concave, so 1 b (log x 1 log x n) log x 1 x n n from which AMGM follows by taking exponents of both sides For other tools, see the formula sheet Peng Shi, Duke University Inequalities, BasicGroup 1 (xz) • (y 3) Group 3 (xy) • (z 3) Group 2 (yz) • (x 3) Bad news !!
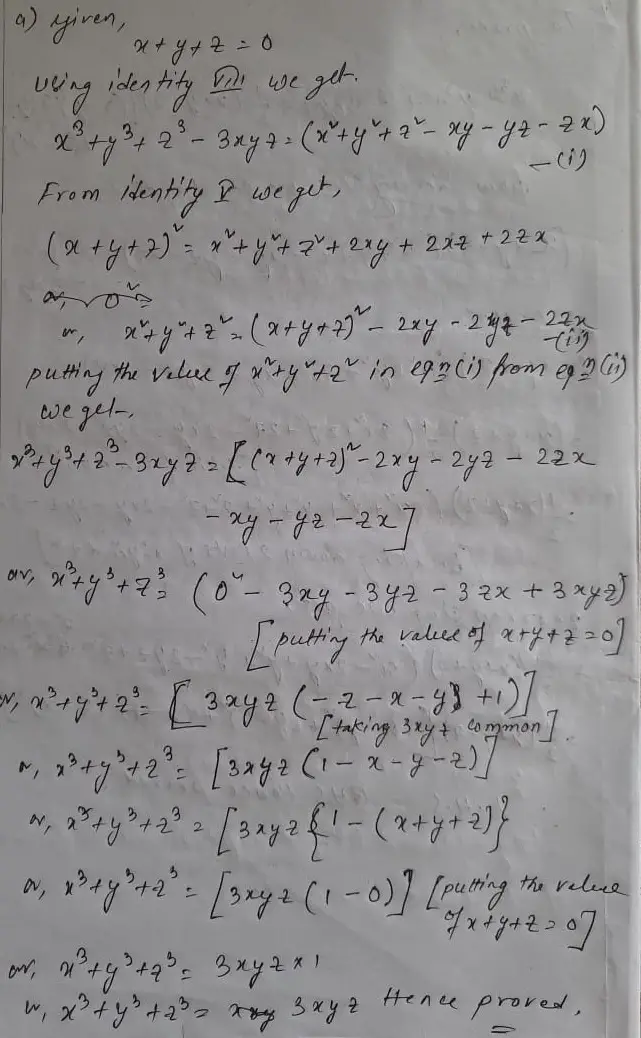



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




Mr Year 14 Problem Column Pdf Triangle Square Root
x 3 y 3 z 33xyz = t k Proof (Piezas) For any rational soln a,b,c,d, one can always find rational p,q,r, For k=1 and a=0, this reduces to the formula for third powers given previously For k=2, this is relevant to equal sums of fifth powers to be discussed later Let's consider the projective surface $S$ over $\mathbb{Q}$ given by $X^3Y^3Z^33XYZW^3=0$ It contains your surface as an open subset, so to answer your question we might as well show that $S(\mathbb{Q})$ is dense in $S(\mathbb{R})$ Observe that $S$ has a singular rational point $P = (1110)$CBSE Syllabus for Class 9 Maths Course Structure First Term Units Unit Marks I Number System 17 II Algebra 25 III Geometry 37 IV Coordinate Geometry 6 V Mensuration 5 Total 90 Second Term Units Unit Marks II Algebra (contd) 16 III Geometry (contd) 38 V Mensuration (contd) 18 VI Statistics 10 VII Probability




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube
When you are clear with the logic behind every formula, solving any kind of problem become easier If you are perfect with all the belowmentioned formulas in Maths for Class 9 that is listed chapterwise, nothing can stop you from scoring maximum marks in the final examinationPARTIAL DIFFERENTIAL EQUATIONS Math 124A { Fall 10 « Viktor Grigoryan grigoryan@mathucsbedu Department of Mathematics University of California, Santa BarbaraAshiprarimandini ashiprarimandini Math Secondary School answered • expert verified If xy z=0 then prove that x 3 y 3 z 3 =3xyz 2 See answers MVB MVB Given, x3 y3 z3 = 3xyz




Prove X3 Y3 Z3 3xyz Or Algebric Formula Dream Of Life Youtube




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com
Notice that each term is a perfect cube x^3 y^3 = (xy)^3 So we have a sum of cubes, and the factoring formula is a^3 b^3 = (ab)(a^2abb^2) So we use a = xy and b = z to get x^3 y^3 z^3 = (xy)^3 z^3 = ((xy) z)((xy)^2(xy)zz^2) =(xy z)(x^2 y^2 xyz z^2) check by multiplying it out to make sure!Find the zeros of the polynomial 4x square 25;Symmetric Polynomials A symmetric polynomial is a polynomial where if you switch any pair of variables, it remains the same For example, y^2x^2z^2 y2 x2 z2 is the same as the initial polynomial Symmetric polynomials can often be found in Vieta's formula and Newton's identities




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz Brainly In




If Math X Y Z 0 Math What Is The Value Of Math Frac X 2 Yz Frac Y 2 Zx Frac Z 2 Xy Math Quora
Answer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website! 16 Note that (can be easily seen with rule of Sarrus) x y z z x y y z x = x3 y3 z3 − 3xyz On the other hand, it is equal to (if we add to the first row 2 other rows) x y z x y z x y z z x y y z x = (x y z)1 1 1 z x y y z x = (x y z)(x2In mathematics, factorization (or factorisation, see English spelling differences) or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kindFor example, 3 × 5 is a factorization of the integer 15, and (x – 2)(x 2) is a factorization of the polynomial x 2 – 4



If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




Tex Verify That X 3 Y 3 Z 3 3xyz Frac 1 2 X Y Z X Brainly In
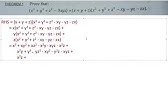
Statement and proof of the Factor Theorem Factorization of ax 2 bx c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem Recall of algebraic expressions and identities Verification of identities (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx (x ± y) 3 = x 3 ± y 3 ± 3xy (x ± y) We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence proved The diophantine equation x^3/3y^3z^32xyz=0 Authors Joseph Amal Nathan Download PDF Abstract We will be presenting two theorems in this paper The first theorem, which is a new result, is about the nonexistence of integer solutions of the cubic diophantine equation In the proof of this theorem we have used some known results from theory of binary cubic forms




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In
Statement and proof of the Factor Theorem x3y3z33xyz LINEAR EQUATIONS IN TWO VARIABLES Examples, problems on Ratio and Proportion UNIT IIICOORDINATE GEOMETRY COORDINATE GEOMETRY No deletion UNIT IVGEOMETRY INTRODUCTION TO EUCLID'S GEOMETRY Delete the Chapter LINES AND ANGLES No deletionThere are two formula of it x^3 y^3 z^3 3xyz = (xyz) (x^2y^2z^2xyyzzx) 2 x^3 y^3 z^3 3xyz = (1/2) (xyz) {xy)^2(yz)^2(zx)^2} if x1/x=5,then find value of x^31/x^3 The valuesof 249square 248square is 729X3512y3 Factorise (abc)³a³b³c3 I need very urgently please answer as quickly as you can Experts, please help me with the following questions attached below in the image Questions are from chapter POLYNOMIALS, grade 9 (please answer all of them




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Factorization Of X3 Y3 Z3 3xyz Youtube




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In




X Y Z 3xyz X Y Z X Y Z Xy Yz Zx Prove Brainly In




Polynomials Ppt Video Online Download




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




If X Y Z 0 Show That X3 Y3 Z3 3xyz Maths Polynomials Meritnation Com



X 3 Y 3 Z 3 3xyz Formula Proof Malaydras




If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Pdf On Solving The Diophantine Equation 𝑥 𝑦 𝑧 𝑘 On A Vector Computer




U Log X 3 Y 3 Z 3 3xyz X Y Z Ux Uy Uz




U Log X 3 Y 3 Z 3 3xyz X Y Z Ux Uy Uz



Www Math Purdue Edu Jlipman Ma598 X 5e3 Y 5e3 Z 5e3 Pdf




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video
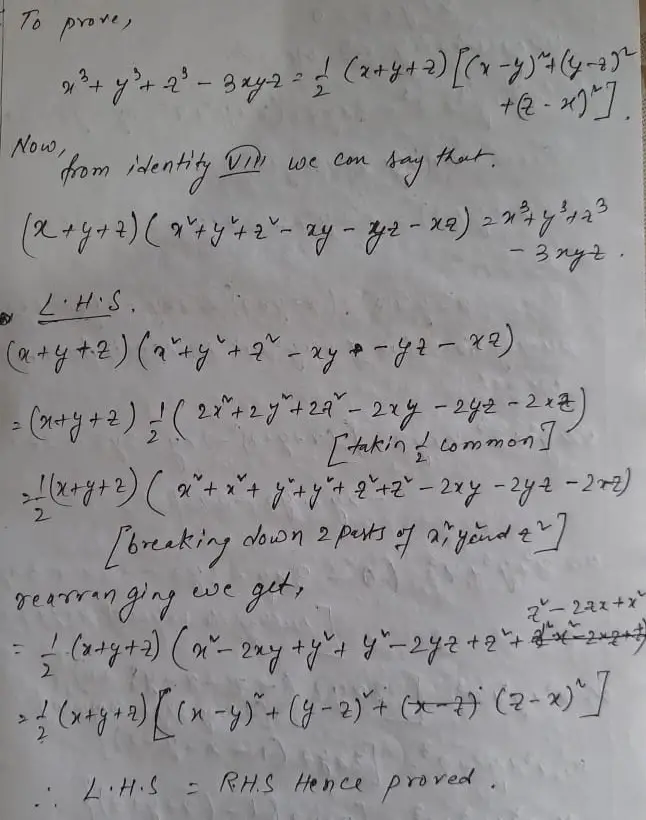



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5



What Is The Solution Of X 3 Y 3 Z 3 Quora




File




If X Y Z 0 Show That X 3 Y 3 Z 3 3x Y Z



If 1 X 1 Y 1 Z 0 And X Y Z 9 Then What Is The Value Of X 3 Y 3 Z 3 3xyz Quora




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Verify Euler S Theorem For The Function U X 3 Y 3 3xy 2 Sarthaks Econnect Largest Online Education Community




Problem Books In Mathematics




1 Pages 1 33 Flip Pdf Download Fliphtml5




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora




Prove That X3 Y3 Z3 3xy X Y Z X2 Y2 Z2 Xy Yz Zx Only By Lhs Brainly In




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




X Y Z 0 Show That X3 Y3 Z3 3xyz Novocom Top




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Bits Of Math Problem Cubes And Cube Roots




If X Y Z 0 Then Show That X3 Y3 Z3 3xyz




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Novocom Top



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5 Studyrankersonline



If Math X Y Z 0 Math How Do You Prove That Math X 3 Y 3 Z 3 3xyz Math Quora




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




F X Y Z




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




If U Log X 2 Y 2 Z 2 Then Prove That X 2 Y 2 Z 2 D 2u Dx 2 D 2u Dy 2 D 2u Dz 2 1



If U Tan 1 X 3 Y 3 X Y Prove That X U X Y U Y Sin 2u Sarthaks Econnect Largest Online Education Community




Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Maths Meritnation Com
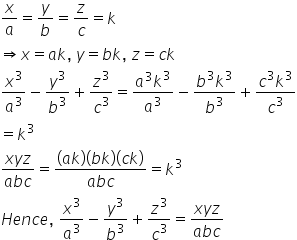



If X A Y B Z C Then Show That X3 A3 Y3 Z3 A Xyz Abc Mathematics Topperlearning Com Mfmw0q55




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044




Ex 2 5 14 Without Actually Calculating The Cubes Find I 12 3




Pdf A Cubic Surface Of Revolution Mark Villarino Academia Edu




Find The Value Of X Cube Y Cube Z Cube Minus 3 X Y Z If X Square Y Square Z Square Is Equal To Brainly In



Arxiv Org Pdf 1301 0243




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z



Search Q X3 Y3 Identity Tbm Isch



If X Y Z 0 How Do You Prove That X3 Y3 Z3 3xyz Quora



If X A Y B Z C Show That X 3 A 3 Y 3 B 3 Z 3 C 3 3xyz Abc Sarthaks Econnect Largest Online Education Community




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




If X Y Z 9 And Xy Yz Zx 23 The Value Of X 3 Y 3 Z 3 3xyz



If X A Y B Z C Show That X 3 A 3 Y 3 B 3 Z 3 C 3 3xyz Abc Sarthaks Econnect Largest Online Education Community




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55



1




Prove That X Y3 Y Z3 Z X3 3x Yy Zz X 2x3 Y3 Z3 3xyz Maths Polynomials Meritnation Com



Search Q X3 2by3 2bz3 3xyz Tbm Isch
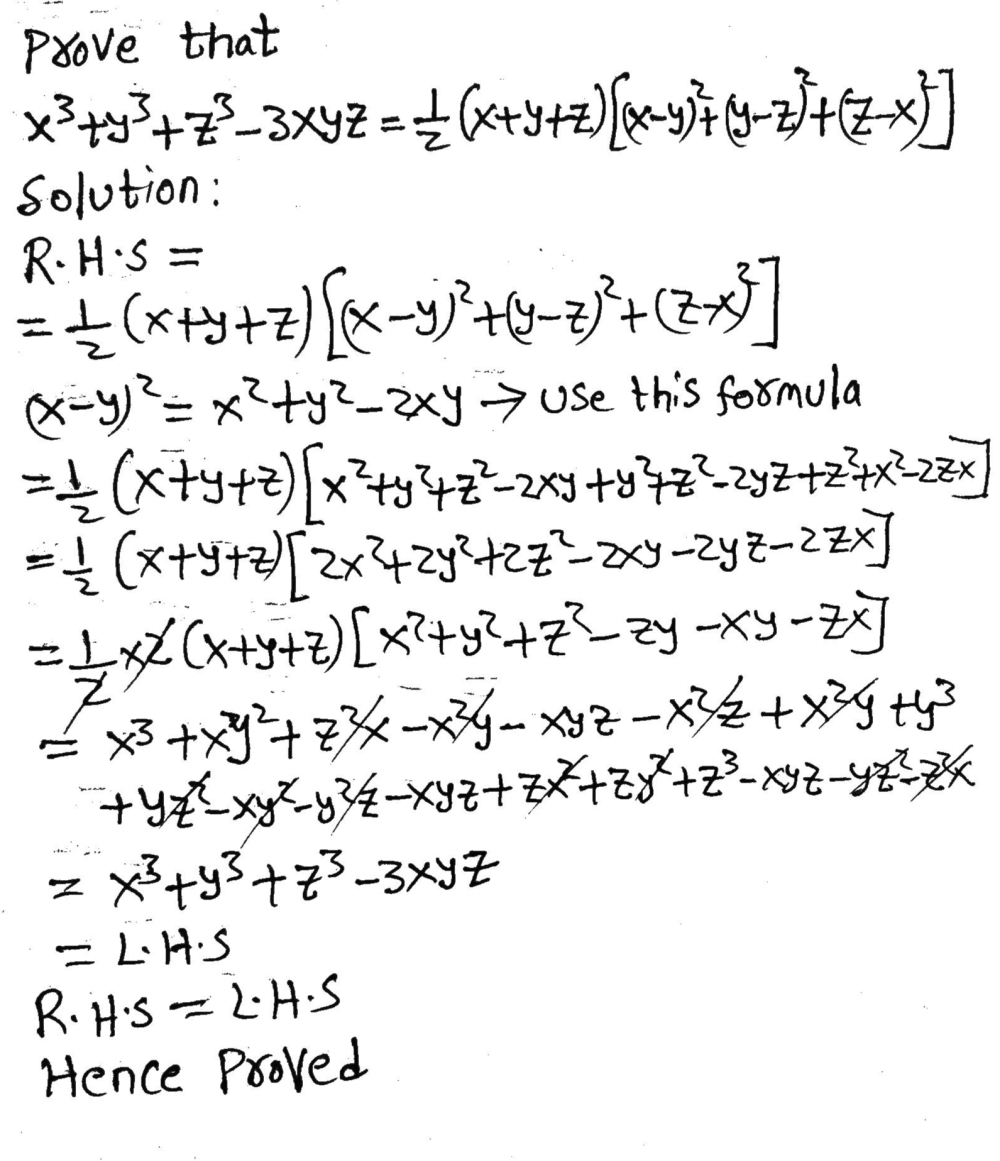



Verify That X 3 Y 3 Z 3 3xyz Frac 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Snapsolve




If X Y Z 6 And Xy Yz Zx 12 Then Show That X 3 Y 3 Z 3 3xyz




Prove That X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Brainly In



Www Jstor Org Stable




X Y Z 0 X3 Y3 Z3 3xyz Novocom Top




2 Two Cube 5 Five Cube 10 Ten Cube Pdf Free Download




Ex 2 5 14 Without Actually Calculating The Cubes Find I 12 3




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Download Free Pdf




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2




48 Mathematics Example 24




यद X Y Z 0 ह त द ख इए क X 3 Y 3 Z 3 3xyz ह Youtube




X Y Z 0 X3 Y3 Z3 3xyz Novocom Top




4 Partial Derivatives And Their Applications Derivative Variable Mathematics




Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2




Mathematics Ii Tranquileducation
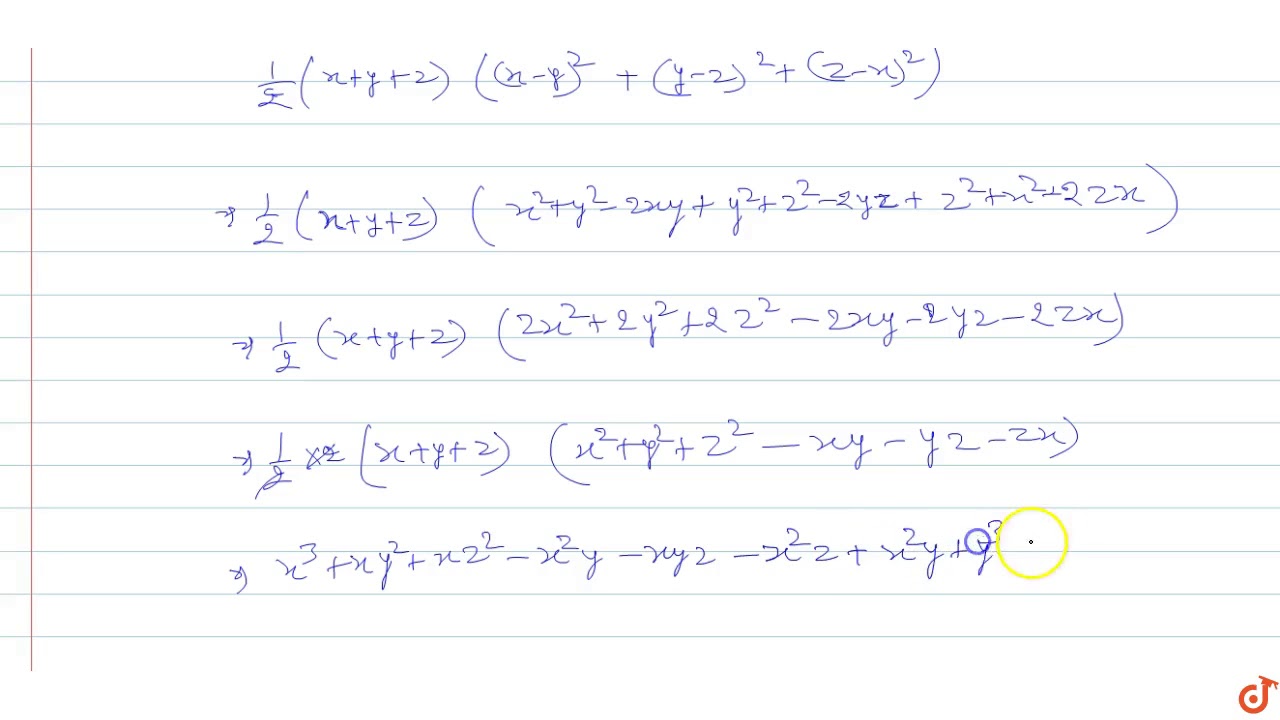



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube



0 件のコメント:
コメントを投稿